Last month I wrote about an interesting geometry trick, that resulted in a rather strange picture. In the post I explained why it happened, but it wasn't completely clear to some of the readers. So I decided to explain it again in a more complete way.
The problem is the following picture:
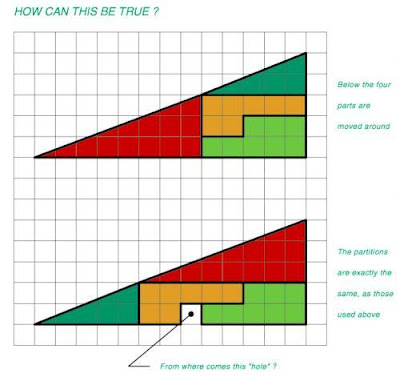
First of all, it should be obvious that the area of both triangles should be equal, because they are built from the some blocks. This means that the missing segment area is still in the picture, but in a different place. Lets look on the following illustration:

In this picture the D dot is moved slightly to create a change in the slope. It is easy to see that the second triangle (on the right) is identical to the first (on the left) but it has another triangle added to it. This is exactly was was done in the original picture. The tiles were rearranged in such a way that the line connecting the points A and C is no longer straight. If the distance that the dot D has moved is small enough we don't see this, and the triangles seem identical.
Lets calculate how much the dot needs to move in order to account for the missing segment area.
In our picture the size of the triangle is: AB=5, BC=13. Thus according to Pythagoras:
The only thing that remains, is to show that indeed in the original picture the slope is different, and that the rearrangement of the pieces creates an extra triangle on top of the original one. This is very simple to do. All you need is to download the image to your computer and open it in an image editing program that supports layers and transparency. Now, cut the bottom triangle and put it in a different layer. Place it above the top triangle and play with transparency. Or you can watch the video below:
The program used to edit the picture is Gimp. It is a free program, capable of replacing Photoshop. The only problem with it is that it is not very intuitive.
I hope this post answered the question. If not, let me know in the comments.







4 comments:
Yes, this new post did explain it in a way I could understand it. Math/geometry has been a subject I never was great at, and the fact I understand is somewhat of a miracle. Thank you.
awesome man! Thank you so much. You solved my problem that I had one decade ago
Dear Anatoly,
Please look at the following diagram:
http://c8.staticflickr.com//9//8463//28314892783_93fe8f577f_z.jpg
The context of this comment is Real analysis, and by using this context series a+b+c+d+...=X , but (as I understand it) since a+b+c+d+...=X one is forced to conclude that 2X=X2√, according to the diagram.
Without loss of generality, let X=1, in this case the considered series is 1/2+1/4+1/8+...
Since the series 1/2+1/4+1/8+... is defined by "zig-zag" lines that all of them have the constant length 2X and it is agreed that 1/2+1/4+1/8+...=1, then the diagram is a proof without words that 1/2+1/4+1/8+...=1 implies 2=2√.
Please prove that a+b+c+d+...=X does not imply 2X=X2√.
Thank you.
@Doron
If I understand you correctly, you are saying that the length of the zigzag line is constant but as the zigzag grows smaller we approach the line of sqrt(2). So if we take a limit, its length must be equal thus getting the 1 = sqrt(2).
The problem here is that you are basically folding the line in each iteration. Using the fact that Q are a dense field, you can indeed fold the line indefinitely, but you are taking the wrong limit in this case. Each iteration, what actually changes is only the area of the triangles, the 'teeth', while the sum of the sides is constant and will not change when you take a limit.
More directly, what you get for the nth iteration of the zigzag is the following sum:
sqrt(n * (2/n)) - length of the line
obviously, the n cancel themselves out.
What actually changes, is their area: 2^-n
Post a Comment